…or is it? A lot of recent papers about diffusion models focus on reducing the number of sampling steps required; some works even aim to enable single-step sampling. That seems counterintuitive, when splitting things up into many easier steps is supposedly why these models work so well in the first place!
In this blog post, let’s take a closer look at the various ways in which the number of sampling steps required to get good results from diffusion models can be reduced. We will focus on various forms of distillation in particular: this is the practice of training a new model (the student) by supervising it with the predictions of another model (the teacher). Various distillation methods for diffusion models have produced extremely compelling results.
I intended this to be relatively high-level when I started writing, but since distillation of diffusion models is a bit of a niche subject, I could not avoid explaining certain things in detail, so it turned into a deep dive. Below is a table of contents. Click to jump directly to a particular section of this post.
- Diffusion sampling: tread carefully!
- Moving through input space with purpose
- Diffusion distillation
- But what about “no free lunch”?
- Do we really need a teacher?
- Charting the maze between data and noise
- Closing thoughts
- Acknowledgements
- References
Diffusion sampling: tread carefully!

First of all, why does it take many steps to get good results from a diffusion model? It’s worth developing a deeper understanding of this, in order to appreciate how various methods are able to cut down on this without compromising the quality of the output – or at least, not too much.
A sampling step in a diffusion model consists of:
- predicting the direction in input space in which we should move to remove noise, or equivalently, to make the input more likely under the data distribution;
- taking a small step in that direction.
Depending on the sampling algorithm, you might add a bit of noise, or use a more advanced mechanism to compute the update direction.
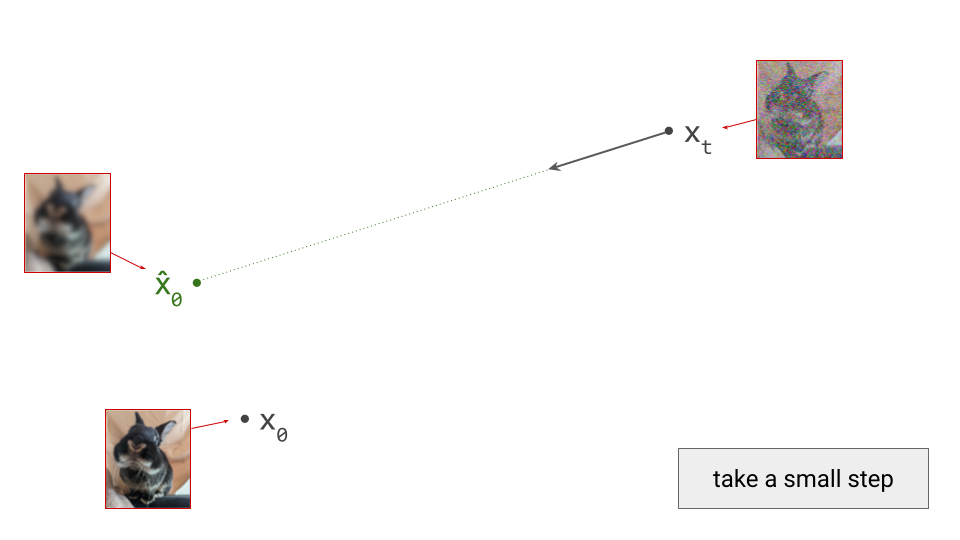
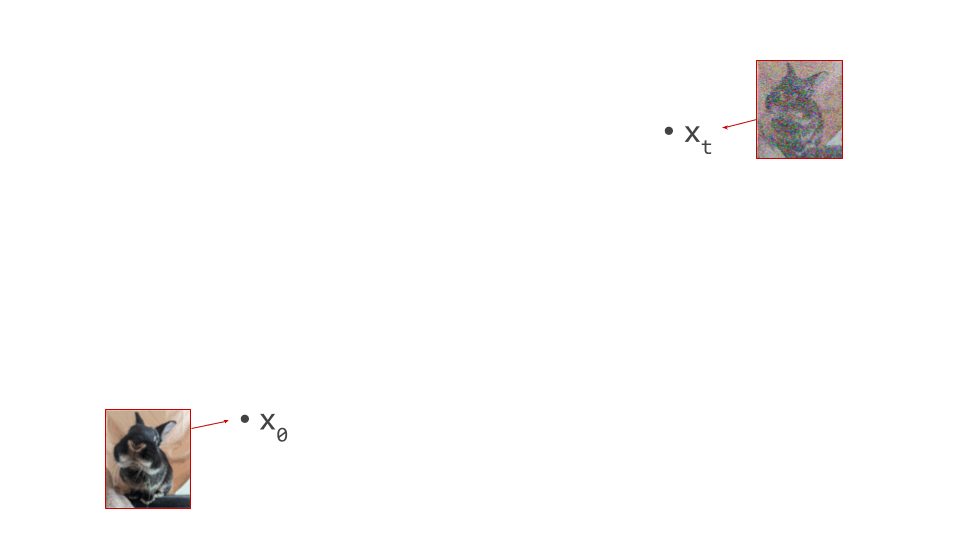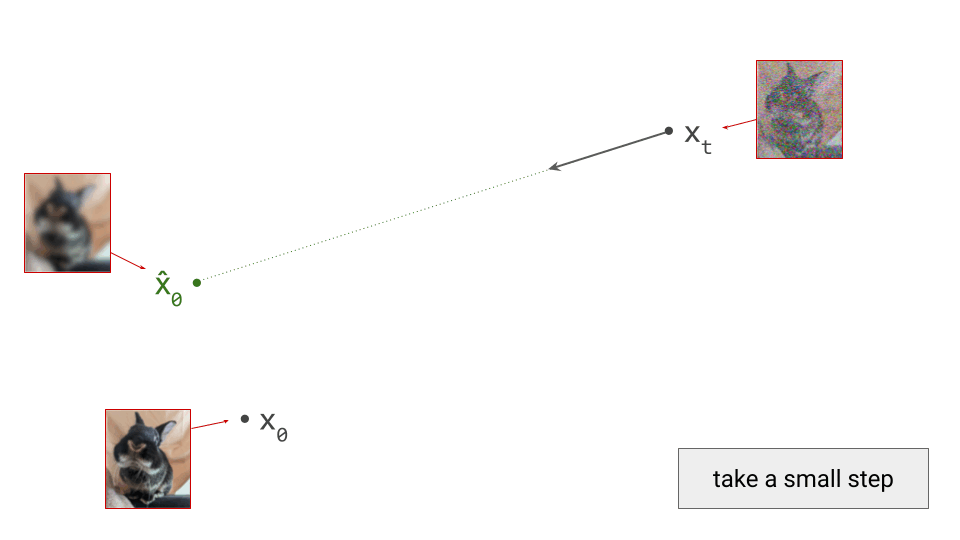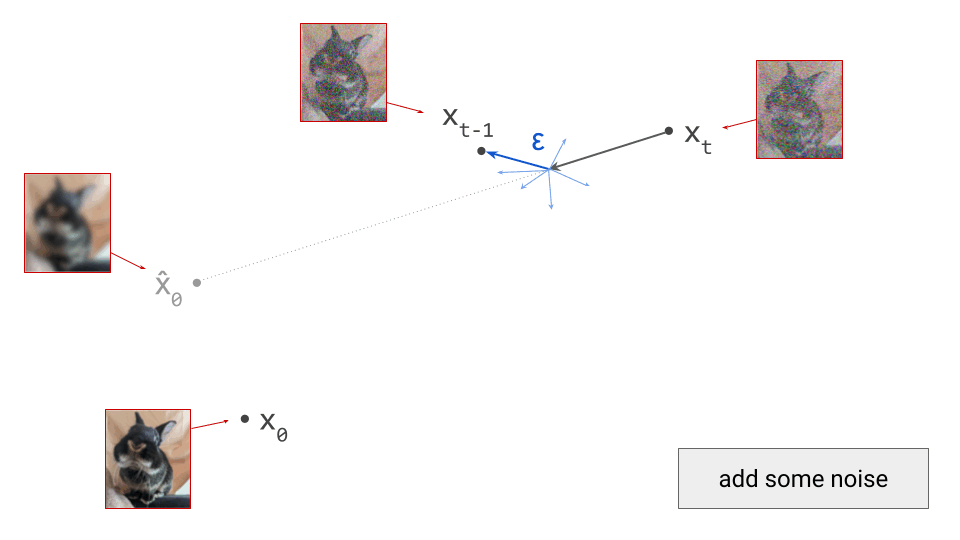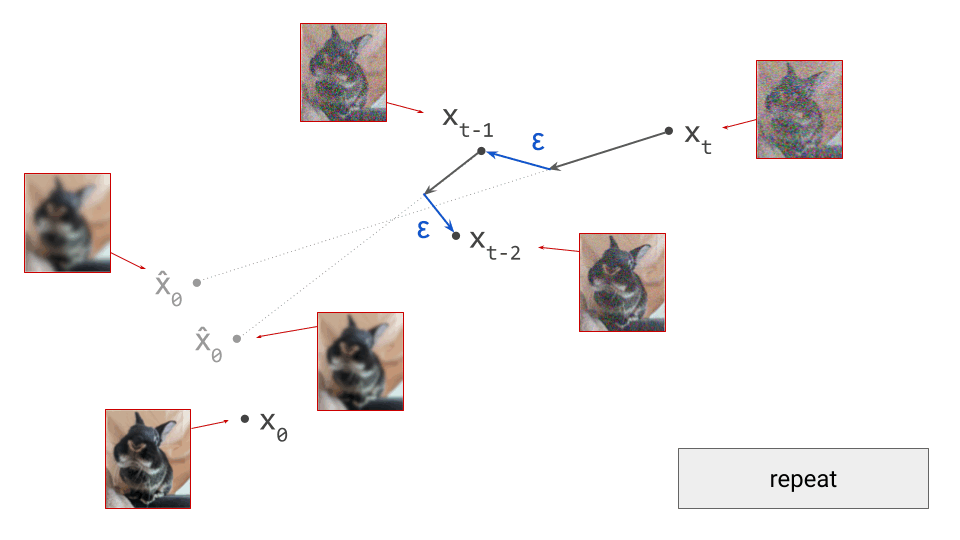
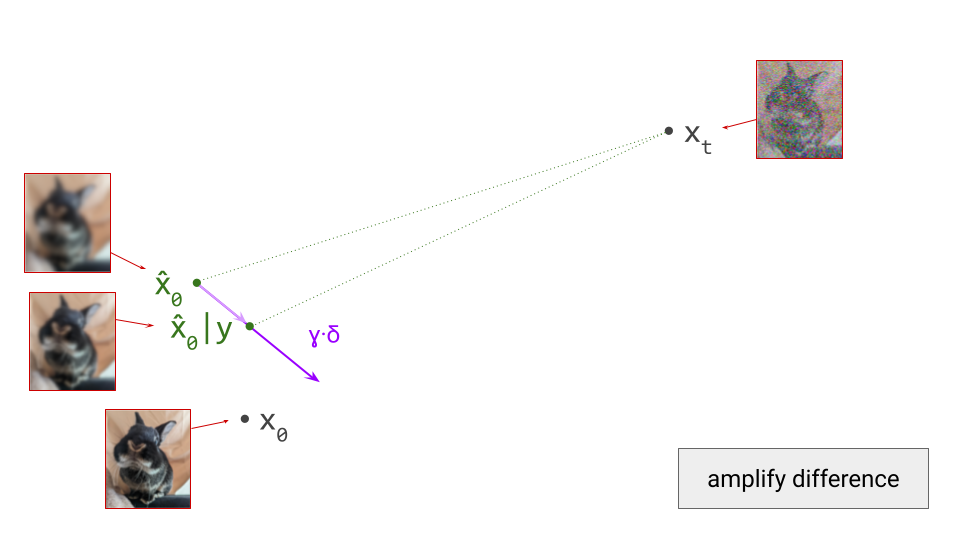
We only take a small step, because this predicted direction is only meaningful locally: it points towards a region of input space where the likelihood under the data distribution is high – not to any specific data point in particular. So if we were to take a big step, we would end up in the centroid of that high-likelihood region, which isn’t necessarily a representative sample of the data distribution. Think of it as a rough estimate. If you find this unintuitive, you are not alone! Probability distributions in high-dimensional spaces often behave unintuitively, something I’ve written an an in-depth blog post about in the past.
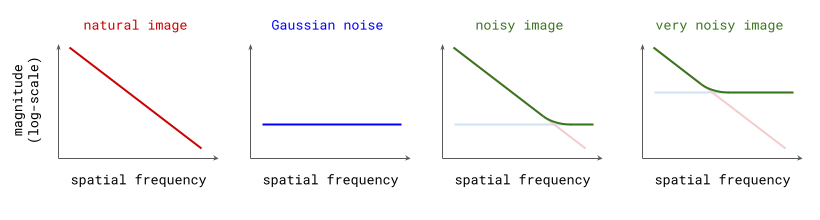
Concretely, in the image domain, taking a big step in the predicted direction tends to yield a blurry image, if there is a lot of noise in the input. This is because it basically corresponds to the average of many plausible images. (For the sake of argument, I am intentionally ignoring any noise that might be added back in as part of the sampling algorithm.)
Another way of looking at it is that the noise obscures high-frequency information, which corresponds to sharp features and fine-grained details (something I’ve also written about before). The uncertainty about this high-frequency information yields a prediction where all the possibilities are blended together, which results in a lack of high-frequency information altogether.
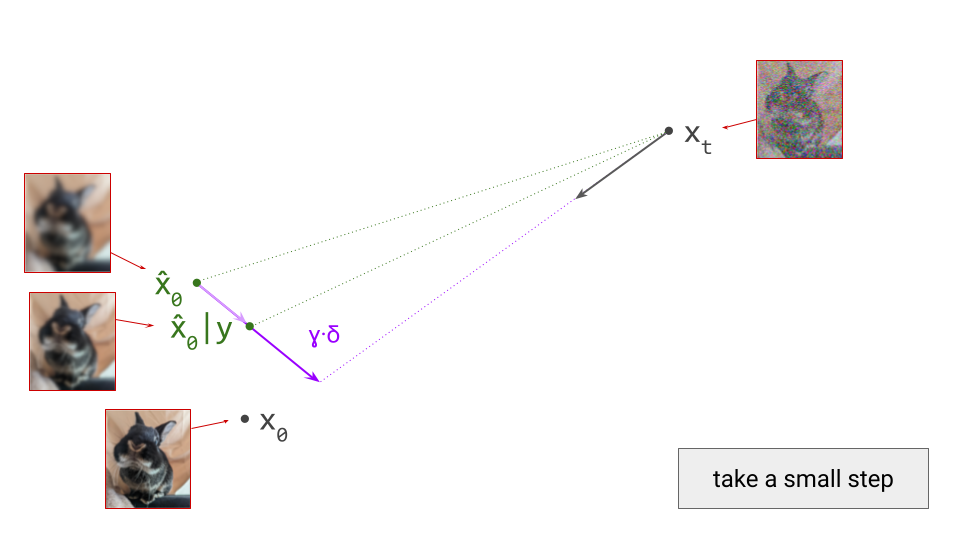
The local validity of the predicted direction implies we should only be taking infinitesimal steps, and then reevaluating the model to determine a new direction. Of course, this is not practical, so we take finite but small steps instead. This is very similar to the way gradient-based optimisation of machine learning models works in parameter space, but here we are operating in the input space instead. Just as in model training, if the steps we take are too large, the quality of the end result will suffer.
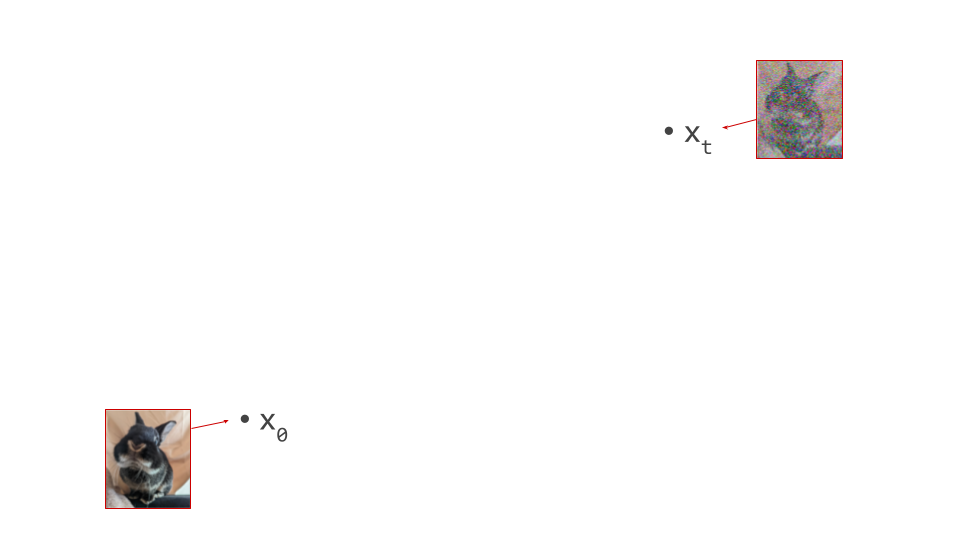
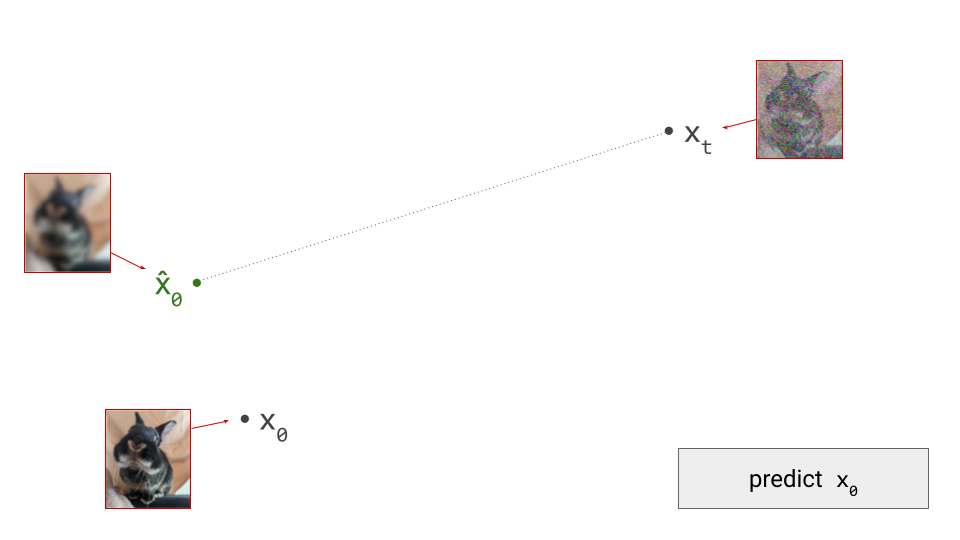
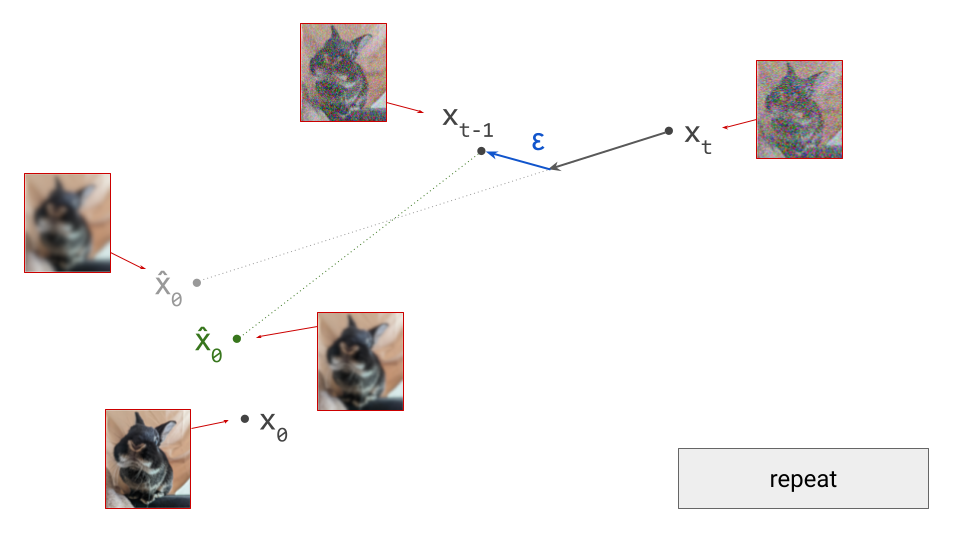
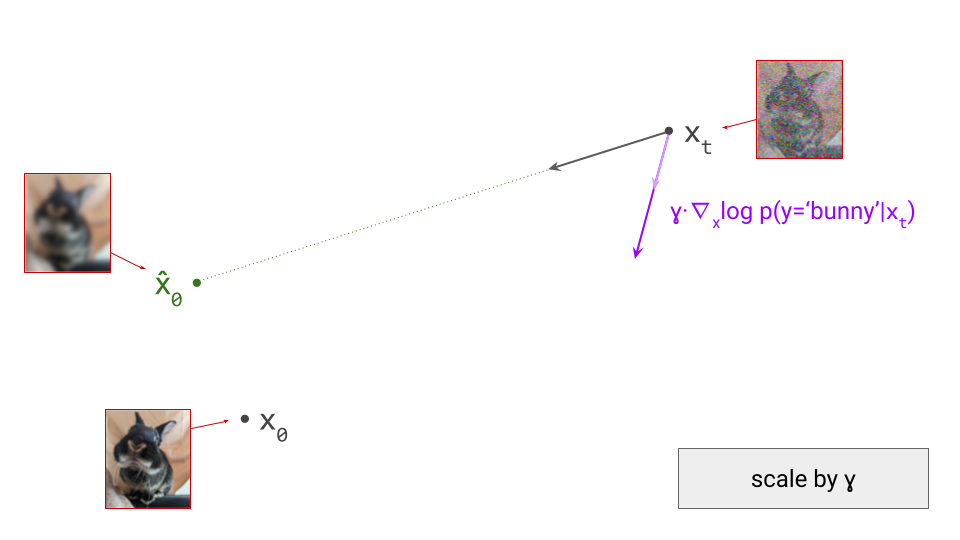
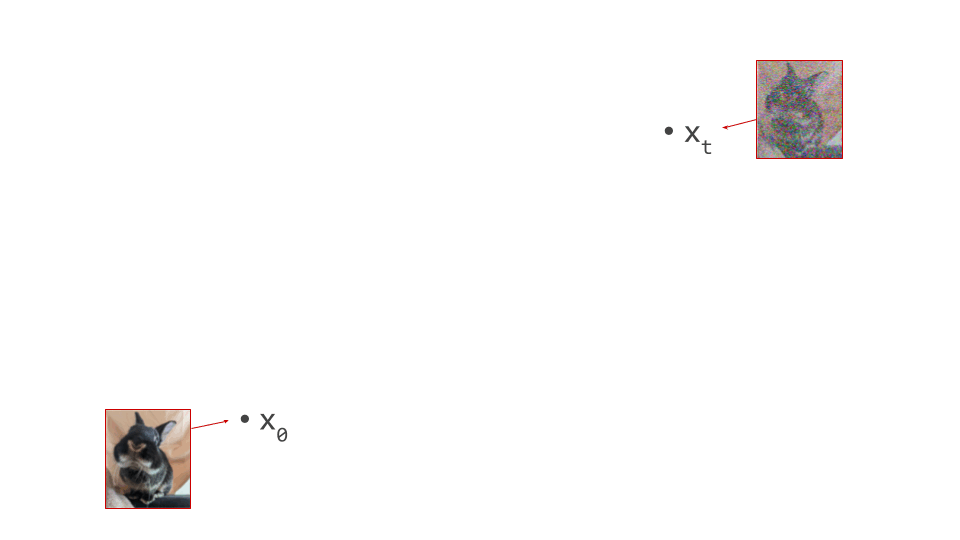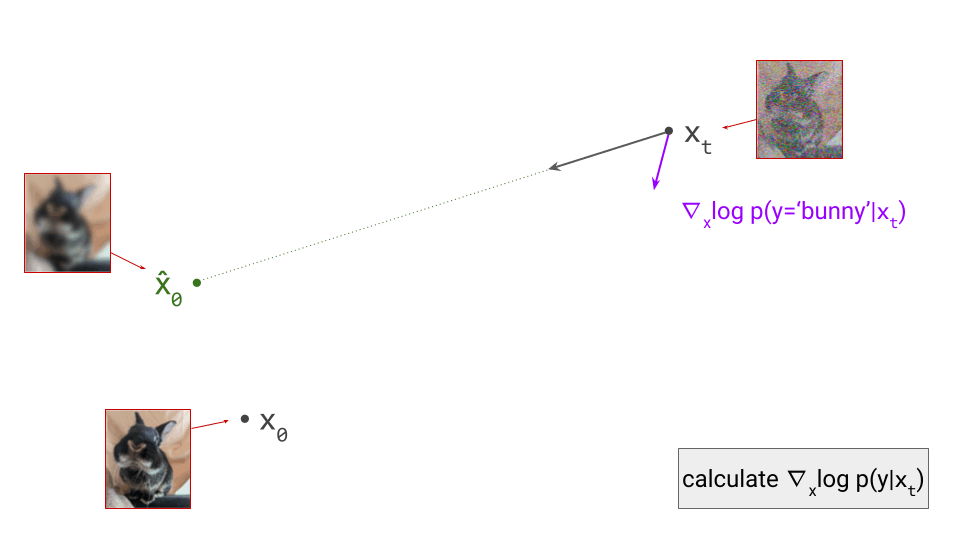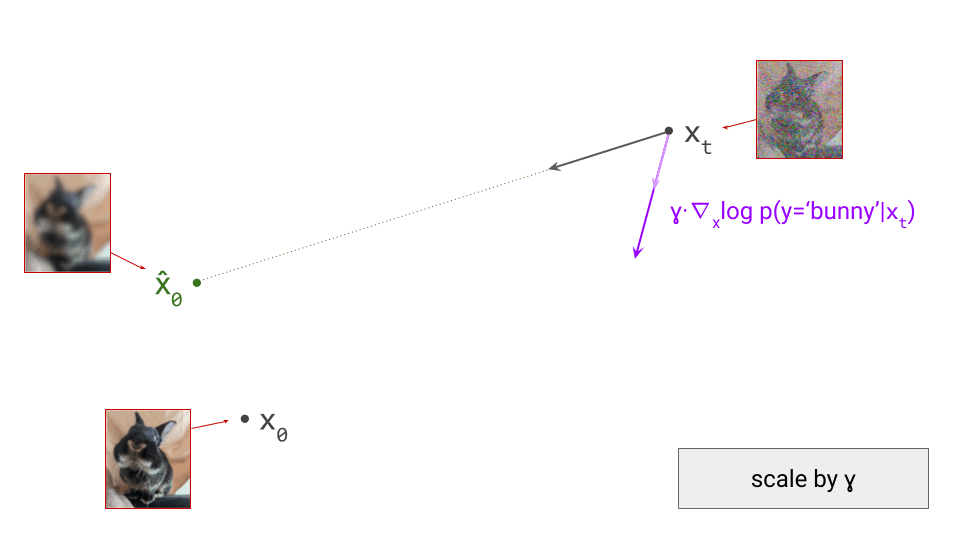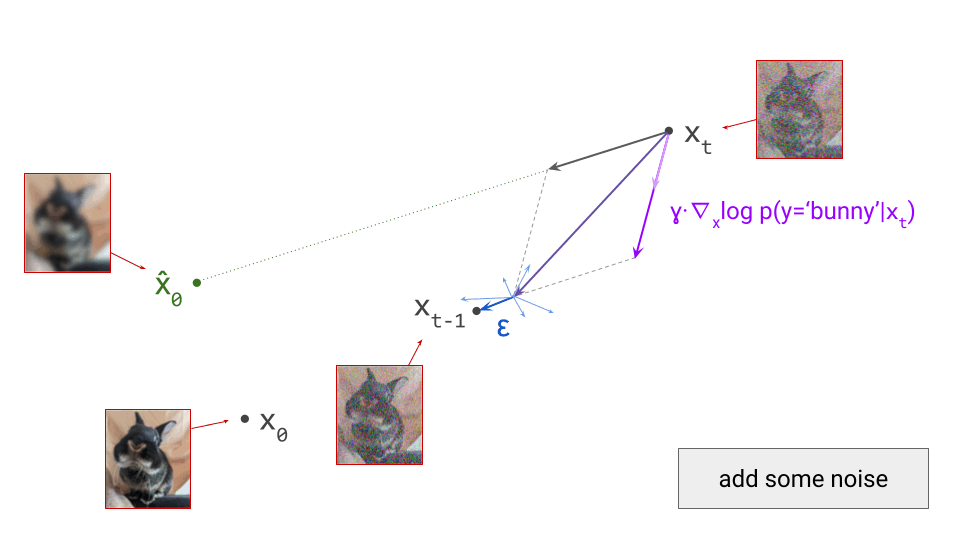
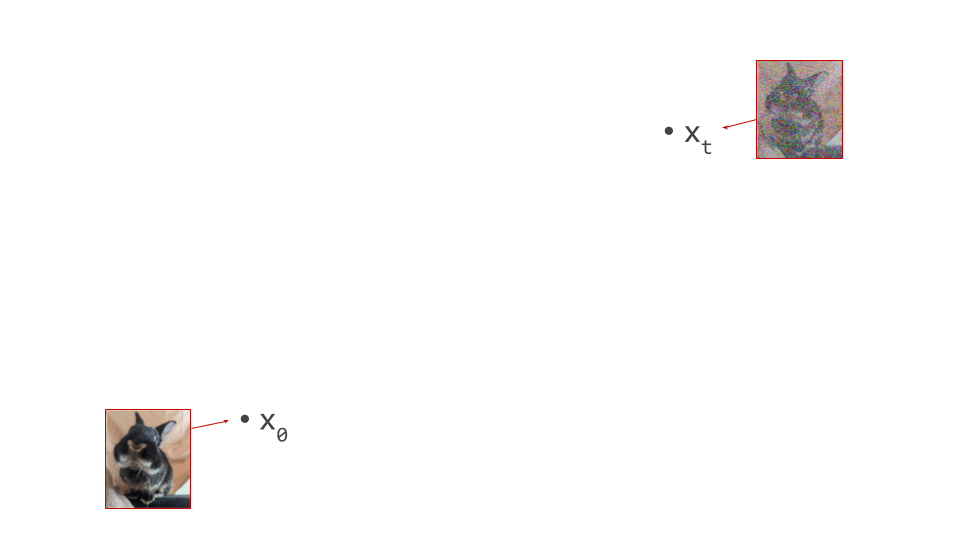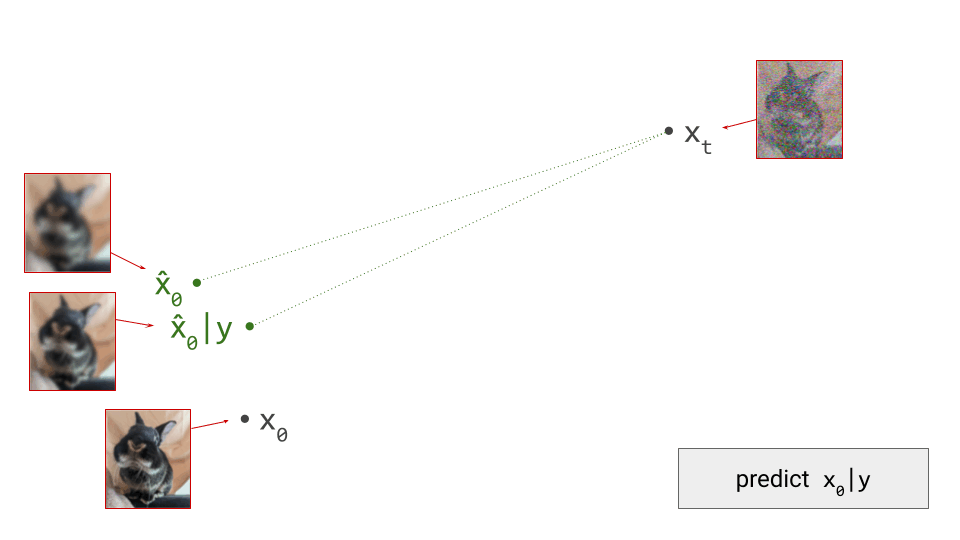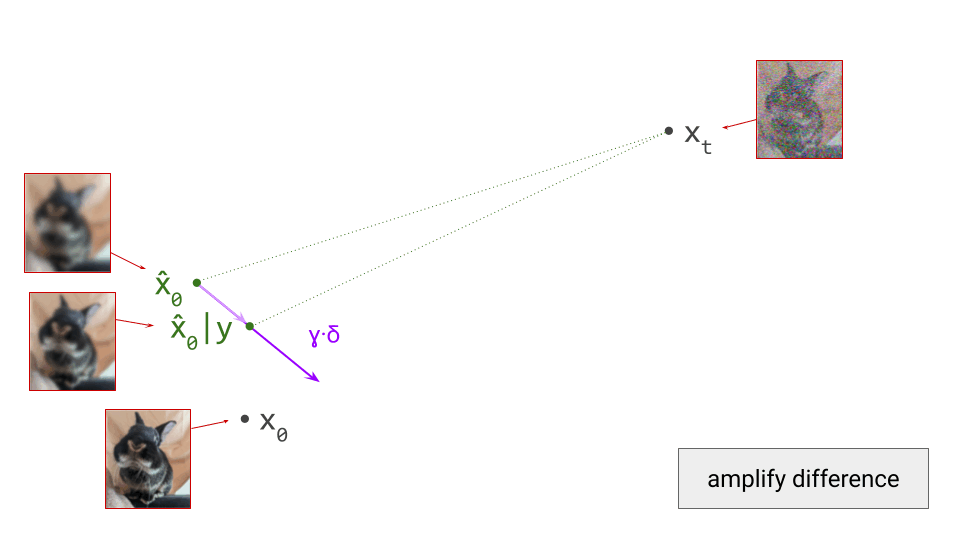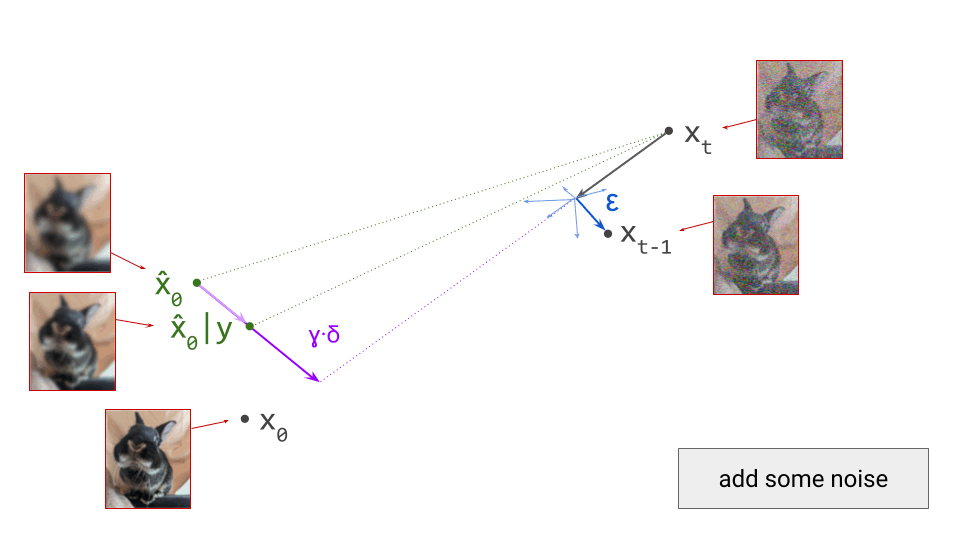
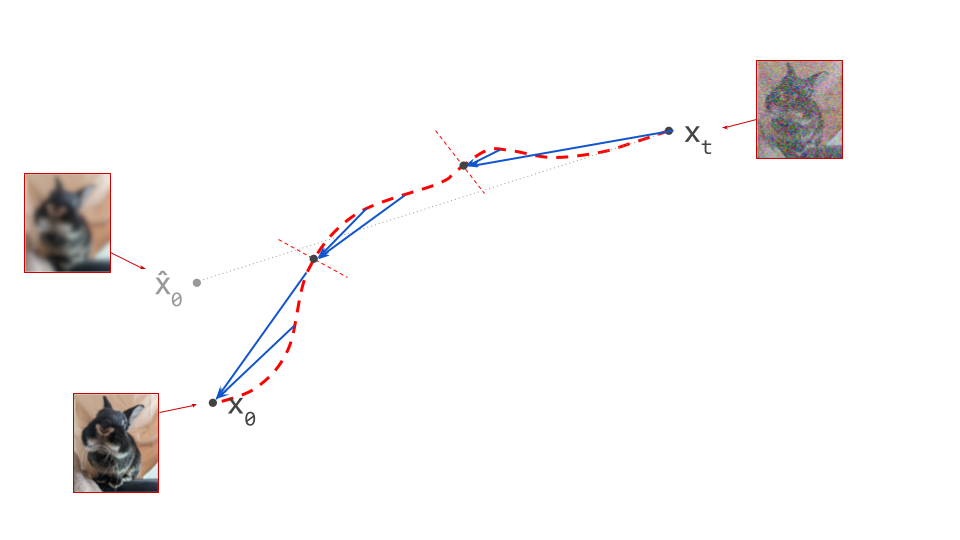
Below is a diagram that represents the input space in two dimensions. \(\mathbf{x}_t\) represents the noisy input at time step \(t\), which we constructed here by adding noise to a clean image \(\mathbf{x}_0\) drawn from the data distribution. Also shown is the direction (predicted by a diffusion model) in which we should move to make the input more likely. This points to \(\hat{\mathbf{x}}_0\), the centroid of a region of high likelihood, which is shaded in pink.
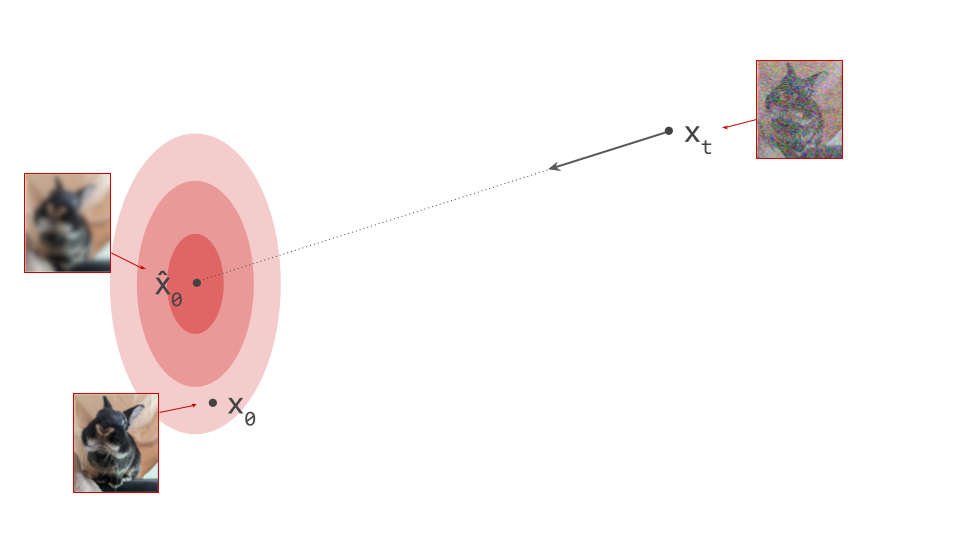
(Please see the first section of my previous blog post on the geometry of diffusion guidance for some words of caution about representing very high-dimensional spaces in 2D!)
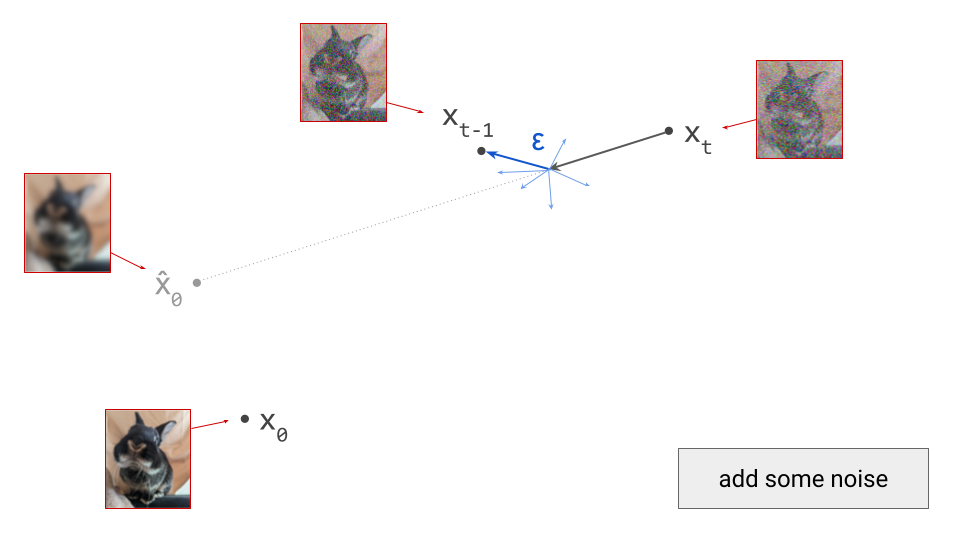
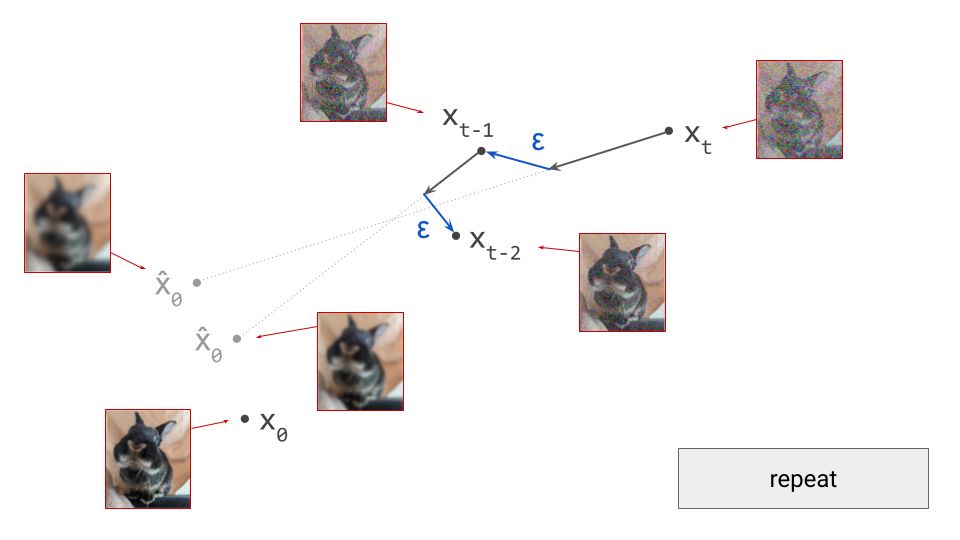
If we proceed to take a step in this direction and add some noise (as we do in the DDPM1 sampling algorithm, for example), we end up with \(\mathbf{x}_{t-1}\), which corresponds to a slightly less noisy input image. The predicted direction now points to a smaller, “more specific” region of high likelihood, because some uncertainty was resolved by the previous sampling step. This is shown in the diagram below.
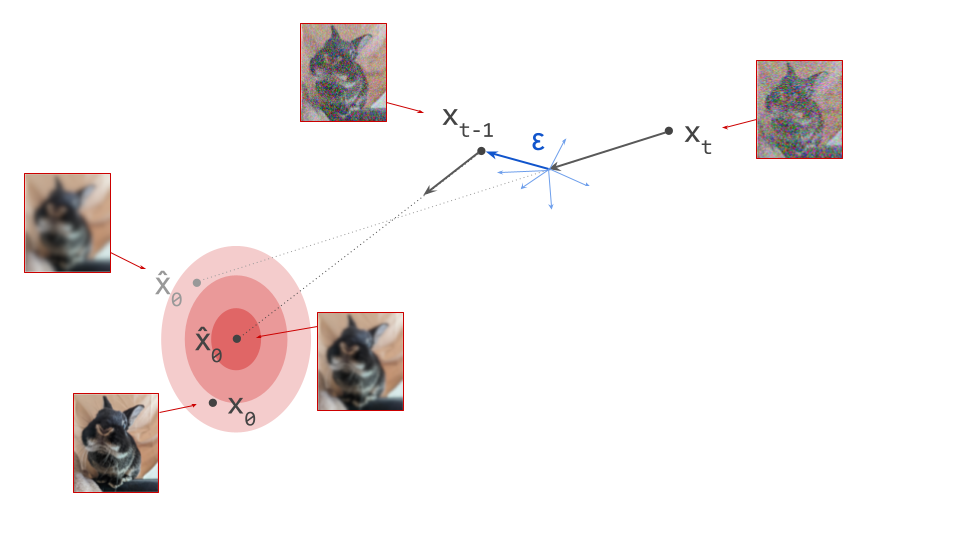
The change in direction at every step means that the path we trace out through input space during sampling is curved. Actually, because we are making a finite approximation, that’s not entirely accurate: it is actually a piecewise linear path. But if we let the number of steps go to infinity, we would end up with a curve. The predicted direction at each point on this curve corresponds to the tangent direction. A stylised version of what this curve might look like is shown in the diagram below.
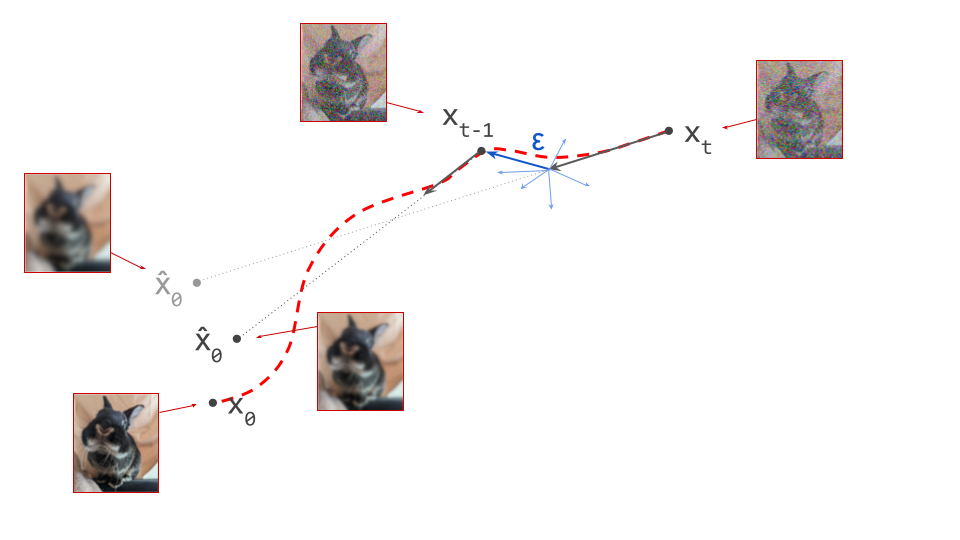
Moving through input space with purpose

A plethora of diffusion sampling algorithms have been developed to move through input space more swiftly and reduce the number of sampling steps required to achieve a certain level of output quality. Trying to list all of them here would be a hopeless endeavour, but I want to highlight a few of these algorithms to demonstrate that a lot of the ideas behind them mimic techniques used in gradient-based optimisation.
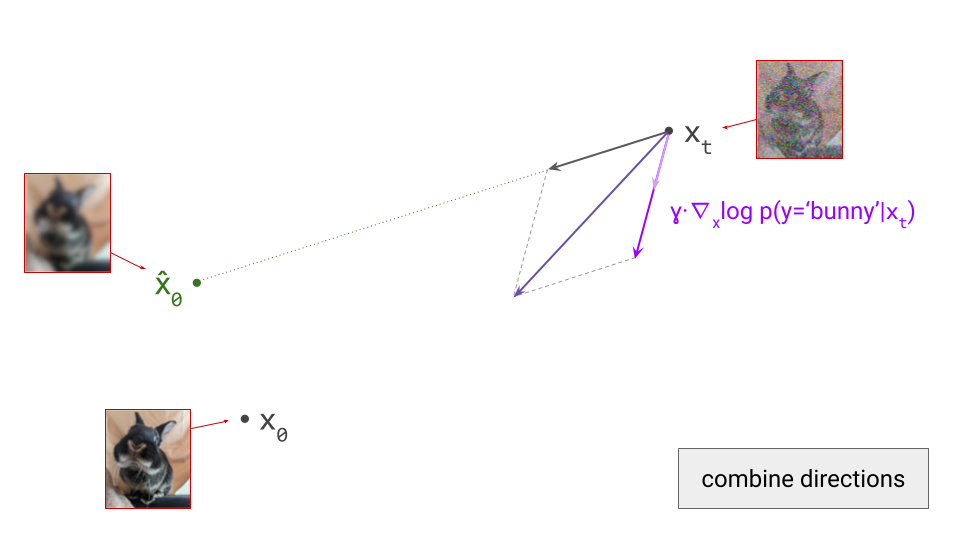
A very common question about diffusion sampling is whether we should be injecting noise at each step, as in DDPM1, and sampling algorithms based on stochastic differential equation (SDE) solvers2. Karras et al.3 study this question extensively (see sections 3 & 4 in their “instant classic” paper) and find that the main effect of introducing stochasticity is error correction: diffusion model predictions are approximate, and noise helps to prevent these approximation errors from accumulating across many sampling steps. In the context of optimisation, the regularising effect of noise in stochastic gradient descent (SGD) is well-studied, so perhaps this is unsurprising.
However, for some applications, injecting randomness at each sampling step is not acceptable, because a deterministic mapping between samples from the noise distribution and samples from the data distribution is necessary. Sampling algorithms such as DDIM4 and ODE-based approaches2 make this possible (I’ve previously written about this feat of magic, as well as how this links together diffusion models and flow-based models). An example of where this comes in handy is for teacher models in the context of distillation (see next section). In that case, other techniques can be used to reduce approximation error while avoiding an increase in the number of sampling steps.
One such technique is the use of higher order methods. Heun’s 2nd order method for solving differential equations results in an ODE-based sampler that requires two model evaluations per step, which it uses to obtain improved estimates of update directions5. While this makes each sampling step approximately twice as expensive, the trade-off can still be favourable in terms of the total number of function evaluations3.
Another variant of this idea involves making the model predict higher-order score functions – think of this as the model estimating both the direction and the curvature, for example. These estimates can then be used to move faster in regions of low curvature, and slow down appropriately elsewhere. GENIE6 is one such method, which involves distilling the expensive second order gradient calculation into a small neural network to reduce the additional cost to a practical level.
Finally, we can emulate the effect of higher-order information by aggregating information across sampling steps. This is very similar to the use of momentum in gradient-based optimisation, which also enables acceleration and deceleration depending on curvature, but without having to explicitly estimate second order quantities. In the context of differential equation solving, this approach is usually termed a multistep method, and this idea has inspired many diffusion sampling algorithms7 8 9 10.
In addition to the choice of sampling algorithm, we can also choose how to space the time steps at which we compute updates. These are spaced uniformly across the entire range by default (think np.linspace), but because noise schedules are often nonlinear (i.e. \(\sigma_t\) is a nonlinear function of \(t\)), the corresponding noise levels are spaced in a nonlinear fashion as a result. However, it can pay off to treat sampling step spacing as a hyperparameter to tune separately from the choice of noise schedule (or, equivalently, to change the noise schedule at sampling time). Judiciously spacing out the time steps can improve the quality of the result at a given step budget3.
Diffusion distillation

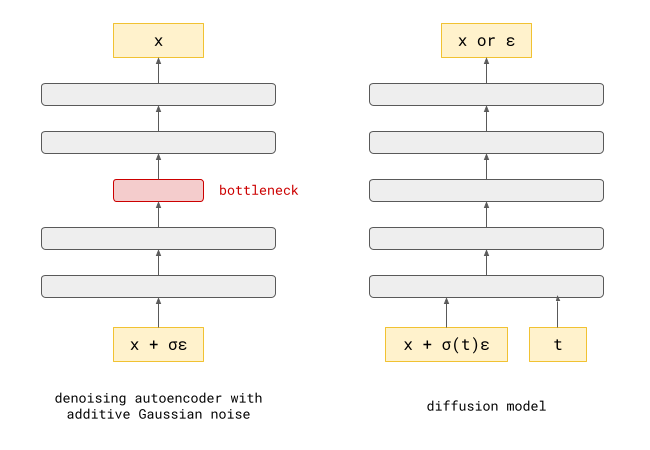
Broadly speaking, in the context of neural networks, distillation refers to training a neural network to mimic the outputs of another neural network11. The former is referred to as the student, while the latter is the teacher. Usually, the teacher has been trained previously, and its weights are frozen. When applied to diffusion models, something interesting happens: even if the student and teacher networks are identical in terms of architecture, the student will converge significantly faster than the teacher did when it was trained.
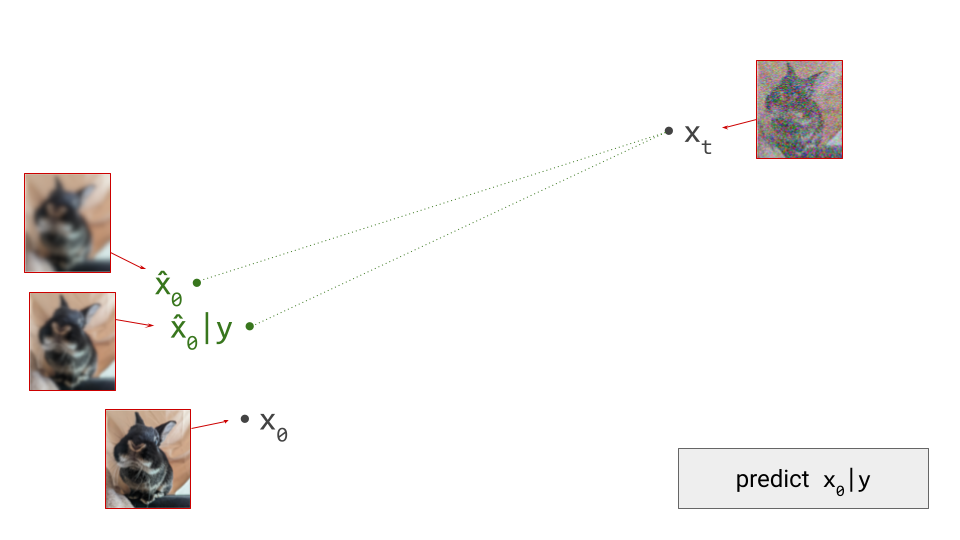
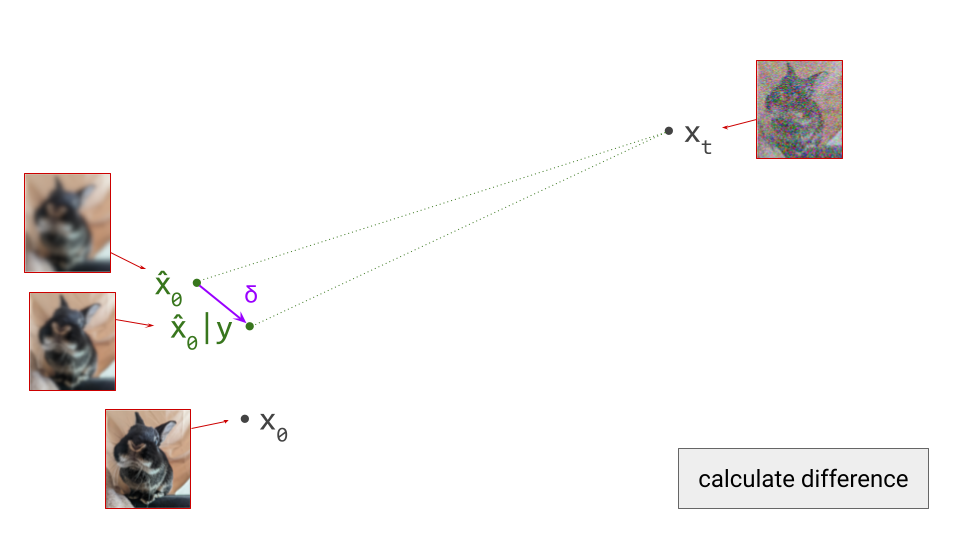
To understand why this happens, consider that diffusion model training involves supervising the network with examples \(\mathbf{x}_0\) from the dataset, to which we have added varying amounts of noise to create the network input \(\mathbf{x}_t\). But rather than expecting the network to be able to predict \(\mathbf{x}_0\) exactly, what we actually want is for it to predict \(\mathbb{E}\left[\mathbf{x}_0 \mid \mathbf{x}_t \right]\), that is, a conditional expectation over the data distribution. It’s worth revisiting the first diagram in section 1 of this post to grasp this: we supervise the model with \(\mathbf{x}_0\), but this is not what we want the model to predict – what we actually want is for it to predict a direction pointing to the centroid of a region of high likelihood, which \(\mathbf{x}_0\) is merely a representative sample of. I’ve previously mentioned this when discussing various perspectives on diffusion. This means that weight updates are constantly pulling the model weights in different directions as training progresses, slowing down convergence.
When we distill a diffusion model, rather than training it from scratch, the teacher provides an approximation of \(\mathbb{E}\left[\mathbf{x}_0 \mid \mathbf{x}_t \right]\), which the student learns to mimic. Unlike before, the target used to supervise the model is now already an (approximate) expectation, rather than a single representative sample. As a result, the variance of the distillation loss is significantly reduced compared to that of the standard diffusion training loss. Whereas the latter tends to produce training curves that are jumping all over the place, distillation provides a much smoother ride. This is especially obvious when you plot both training curves side by side. Note that this variance reduction does come at a cost: since the teacher is itself an imperfect model, we’re actually trading variance for bias.
Variance reduction alone does not explain why distillation of diffusion models is so popular, however. Distillation is also a very effective way to reduce the number of sampling steps required. It seems to be a lot more effective in this regard than simply changing up the sampling algorithm, but of course there is also a higher upfront cost, because it requires additional model training.
There are many variants of diffusion distillation, a few of which I will try to compactly summarise below. It goes without saying that this is not an exhaustive review of the literature. A relatively recent survey paper is Weijian Luo’s (from April 2023)12, though a lot of work has appeared in this space since then, so I will try to cover some newer things as well. If you feel there is a particular method that’s worth mentioning but that I didn’t cover, let me know in the comments.
Distilling diffusion sampling into a single forward pass
A typical diffusion sampling procedure involves repeatedly applying a neural network on a canvas, and using the prediction to update that canvas. When we unroll the computational graph of this network, this can be reinterpreted as a much deeper neural network in its own right, where many layers share weights. I’ve previously discussed this perspective on diffusion in more detail.
Distillation is often used to compress larger networks into smaller ones, so Luhman & Luhman13 set out to train a much smaller student network to reproduce the outputs of this much deeper teacher network corresponding to an unrolled sampling procedure. In fact, what they propose is to distill the entire sampling procedure into a network with the same architecture used for a single diffusion prediction step, by matching outputs in the least-squares sense (MSE loss). Depending on how many steps the sampling procedure has, this may correspond to quite an extreme form of model compression (in the sense of compute, that is – the number of parameters stays the same, of course).
This approach requires a deterministic sampling procedure, so they use DDIM4 – a choice which many distillation methods that were developed later also follow. The result of their approach is a compact student network which transforms samples from the noise distribution into samples from the data distribution in a single forward pass.
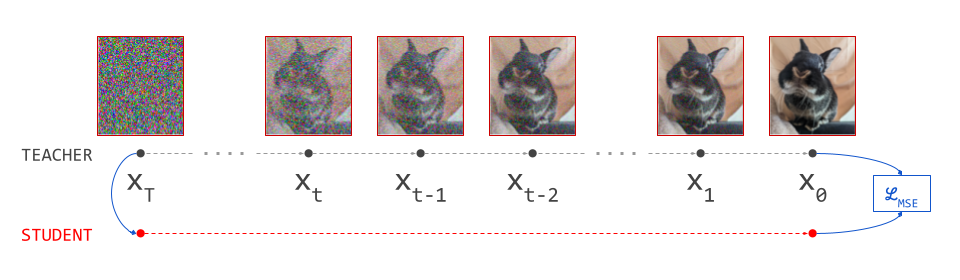
Putting this into practice, one encounters a significant hurdle, though: to obtain a single training example for the student, we have to run the full diffusion sampling procedure using the teacher, which is usually too expensive to do on-the-fly during training. Therefore the dataset for the student has to be pre-generated offline. This is still expensive, but at least it only has to be done once, and the resulting training examples can be reused for multiple epochs.
To speed up the learning process, it also helps to initialise the student with the weights of the teacher (which we can do because their architectures are identical). This is a trick that most diffusion distillation methods make use of.
This work served as a compelling proof-of-concept for diffusion distillation, but aside from the computational cost, the accumulation of errors in the deterministic sampling procedure, combined with the approximate nature of the student predictions, imposed significant limits on the achievable output quality.
Progressive distillation
Progressive distillation14 is an iterative approach that halves the number of required sampling steps. This is achieved by distilling the output of two consecutive sampling steps into a single forward pass. As with the previous method, this requires a deterministic sampling method (the paper uses DDIM), as well as a predetermined number of sampling steps \(N\) to use for the teacher model.
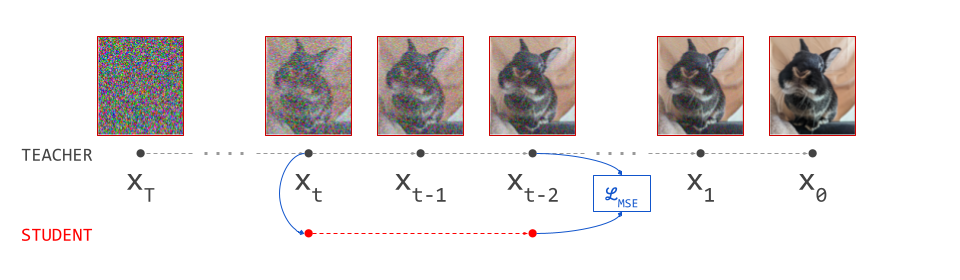
To reduce the number of sampling steps further, it can be applied repeatedly. In theory, one can go all the way down to single-step sampling by applying the procedure \(\log_2 N\) times. This addresses several shortcomings of the previous approach:
- At each distillation stage, only two consecutive sampling steps are required, which is significantly cheaper than running the whole sampling procedure end-to-end. Therefore it can be done on-the-fly during training, and pre-generating the training dataset is no longer required.
- The original training dataset used for the teacher model can be reused, if it is available (or any other dataset!). This helps to focus learning on the part of input space that is relevant and interesting.
- While we could go all the way down to 1 step, the iterative nature of the procedure enables a trade-off between quality and compute cost. Going down to 4 or 8 steps turns out to help a lot to keep the inevitable quality loss from distillation at bay, while still speeding up sampling very significantly. This also provides a much better trade-off than simply reducing the number of sampling steps for the teacher model, instead of distilling it (see Figure 4 in the paper).
Aside: v-prediction
The most common parameterisation for training diffusion models in the image domain, where the neural network predicts the standardised Gaussian noise variable \(\varepsilon\), causes problems for progressive distillation. The implicit relative weighting of noise levels in the MSE loss w.r.t. \(\varepsilon\) is particularly suitable for visual data, because it maps well to the human visual system’s varying sensitivity to low and high spatial frequencies. This is why it is so commonly used.
To obtain a prediction in input space \(\hat{\mathbf{x}}_0\) from a model that predicts \(\varepsilon\) from the noisy input \(\mathbf{x}_t\), we can use the following formula:
\[\hat{\mathbf{x}}_0 = \alpha_t^{-1} \left( \mathbf{x}_t - \sigma_t \varepsilon (\mathbf{x}_t) \right) .\]Here, \(\sigma_t\) represents the standard deviation of the noise at time step \(t\). (For variance-preserving diffusion, the scale factor \(\alpha_t = \sqrt{1 - \sigma_t^2}\), for variance-exploding diffusion, \(\alpha_t = 1\).)
At high noise levels, \(\mathbf{x}_t\) is dominated by noise, so the difference between \(\mathbf{x}_t\) and the scaled noise prediction is potentially quite small – but this difference entirely determines the prediction in input space \(\hat{\mathbf{x}}_0\)! This means any prediction errors may get amplified. In standard diffusion models, this is not a problem in practice, because errors can be corrected over many steps of sampling. In progressive distillation, this becomes a problem in later iterations, where we mainly evaluate the model at high noise levels (in the limit of a single-step model, the model is only ever evaluated at the highest noise level).
It turns out this issue can be addressed simply by parameterising the model to predict \(\mathbf{x}_0\) instead, but the progressive distillation paper also introduces a new prediction target \(\mathbf{v} = \alpha_t \varepsilon - \sigma_t \mathbf{x}_0\) (“velocity”, see section 4 and appendix D). This has some really nice properties, and has also become quite popular beyond just distillation applications in recent times.
Guidance distillation
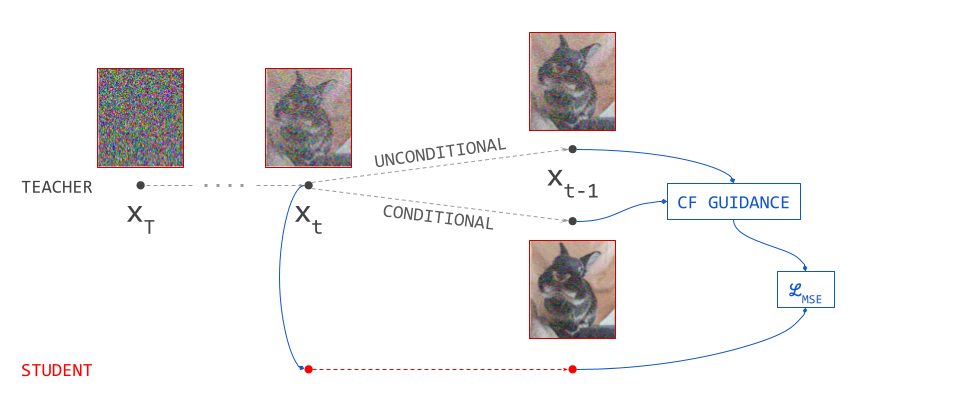
Before moving on to more advanced diffusion distillation methods that reduce the number of sampling steps, it’s worth looking at guidance distillation. The goal of this method is not to achieve high-quality samples in fewer steps, but rather to make each step computationally cheaper when using classifier-free guidance15. I have already dedicated two entire blog posts specifically to diffusion guidance, so I will not recap the concept here. Check them out first if you’re not familiar:
The use of classifier-free guidance requires two model evaluations per sampling step: one conditional, one unconditional. This makes sampling roughly twice as expensive, as the main cost is in the model evaluations. To avoid paying that cost, we can distill predictions that result from guidance into a model that predicts them directly in a single forward pass, conditioned on the chosen guidance scale16.
While guidance distillation does not reduce the number of sampling steps, it roughly halves the required computation per step, so it still makes sampling roughly twice as fast. It can also be combined with other forms of distillation. This is useful, because reducing the number of sampling steps actually reduces the impact of guidance, which relies on repeated small adjustments to update directions to work. Applying guidance distillation before another distillation method can help ensure that the original effect is preserved as the number of steps is reduced.
Rectified flow
One way to understand the requirement for diffusion sampling to take many small steps, is through the lens of curvature: we can only take steps in a straight line, so if the steps we take are too large, we end up “falling off” the curve, leading to noticeable approximation errors.
As mentioned before, some sampling algorithms compensate for this by using curvature information to determine the step size, or by injecting noise to reduce error accumulation. The rectified flow method17 takes a more drastic approach: what if we just replace these curved paths between samples from the noise and data distributions with another set of paths that are significantly less curved?
This is possible using a procedure that resembles distillation, though it doesn’t quite have the same goal: whereas distillation tries to learn better/faster approximations of existing paths between samples from the noise and data distributions, the reflow procedure replaces the paths with a new set of paths altogether. We get a new model that gives rise to a set of paths with a lower cost in the “optimal transport” sense. Concretely, this means the paths are less curved. They will also typically connect different pairs of samples than before. In some sense, the mapping from noise to data is “rewired” to be more straight.
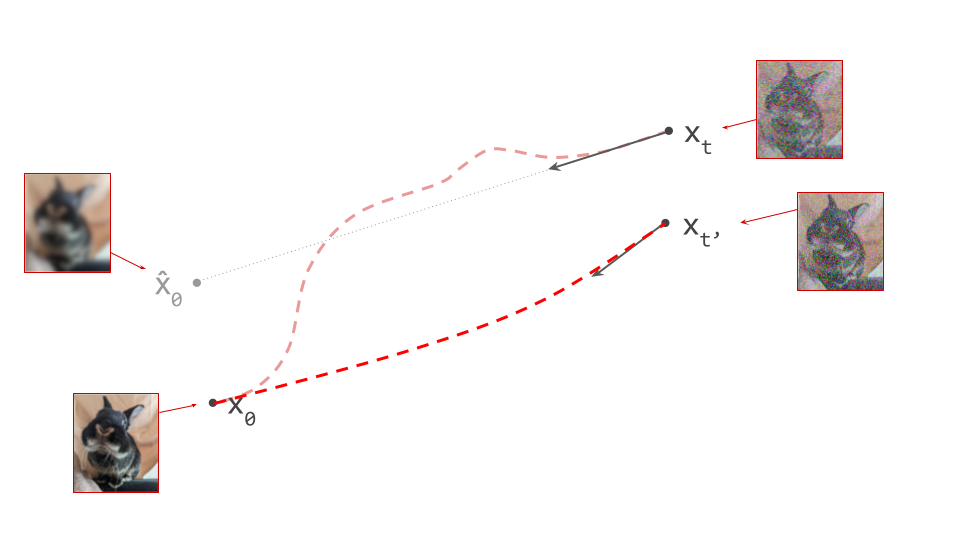
Lower curvature means we can take fewer, larger steps when sampling from this new model using our favourite sampling algorithm, while still keeping the approximation error at bay. But aside from that, this also greatly increases the efficacy of distillation, presumably because it makes the task easier.
The procedure can be applied recursively, to yield and even straighter set of paths. After an infinite number of applications, the paths should be completely straight. In practice, this only works up to a certain point, because each application of the procedure yields a new model which approximates the previous, so errors can quickly accumulate. Luckily, only one or two applications are needed to get paths that are mostly straight.
This method was successfully applied to a Stable Diffusion model18 and followed by a distillation step using a perceptual loss19. The resulting model produces reasonable samples in a single forward pass. One downside of the method is that each reflow step requires the generation of a dataset of sample pairs (data and corresponding noise) using a deterministic sampling algorithm, which usually needs to be done offline to be practical.
Consistency distillation & TRACT
As we covered before, diffusion sampling traces a curved path through input space, and at each point on this curve, the diffusion model predicts the tangent direction. What if we had a model that could predict the endpoint of the path on the side of the data distribution instead, allowing us to jump there from anywhere on the path in one step? Then the degree of curvature simply wouldn’t matter.
This is what consistency models20 do. They look very similar to diffusion models, but they predict a different kind of quantity: an endpoint of the path, rather than a tangent direction. In a sense, diffusion models and consistency models are just two different ways to describe a mapping between noise and data. Perhaps it could be useful to think of consistency models as the “integral form” of diffusion models (or, equivalently, of diffusion models as the “derivative form” of consistency models).
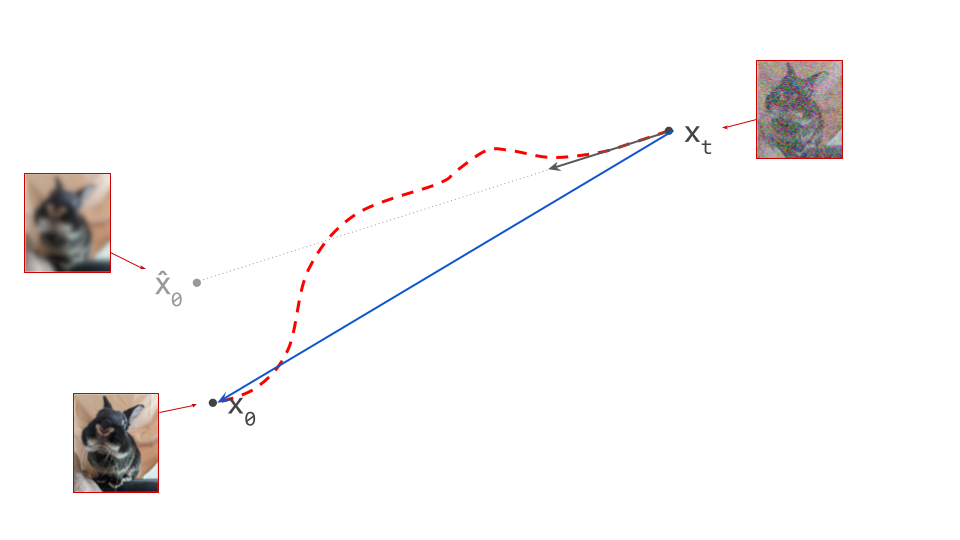
While it is possible to train a consistency model from scratch (though not that straightforward, in my opinion – more on this later), a more practical route to obtaining a consistency model is to train a diffusion model first, and then distill it. This process is called consistency distillation.
It’s worth noting that the resulting model looks quite similar to what we get when distilling the diffusion sampling procedure into a single forward pass. However, that only lets us jump from one endpoint of a path (at the noise side) to the other (at the data side). Consistency models are able to jump to the endpoint on the data side from anywhere on the path.
Learning to map any point on a path to its endpoint requires paired data, so it would seem that we once again need to run the full sampling process to obtain training targets from the teacher model, which is expensive. However, this can be avoided using a bootstrapping mechanism where, in addition to learning from the teacher, the student also learns from itself.
This hinges on the following principle: the prediction of the consistency model along all points on the path should be the same. Therefore, if we take a step along the path using the teacher, the student’s prediction should be unchanged. Let \(f(\mathbf{x}_t, t)\) represent the student (a consistency model), then we have:
\[f(\mathbf{x}_{t - \Delta t}, t - \Delta t) \equiv f(\mathbf{x}_t, t),\]where \(\Delta t\) is the step size and \(\mathbf{x}_{t - \Delta t}\) is the result of a sampling step starting from \(\mathbf{x}_t\), with the update direction given by the teacher. The prediction remains consistent along all points on the path, which is where the name comes from. Note that this is not at all true for diffusion models.
Concurrently with the consistency models paper, transitive closure time-distillation (TRACT)21 was proposed as an improvement over progressive distilation, using a very similar bootstrapping mechanism. The details of implementation differ, and rather than predicting the endpoint of a path from any point on the path, as consistency models do, TRACT instead divides the range of time steps into intervals, with the distilled model predicting points on paths at the boundaries of those intervals.
Like progressive distillation, this is a procedure that can be repeated with fewer and fewer intervals, to eventually end up with something that looks pretty much the same as a consistency model (when using a single interval that encompasses the entire time step range). TRACT was proposed as an alternative to progressive distillation which requires fewer distillation stages, thus reducing the potential for error accumulation.
It is well-known that diffusion models benefit significantly from weight averaging22 23, so both TRACT and the original formulation of consistency models use an exponential moving average (EMA) of the student’s weights to construct a self-teacher model, which effectively acts as an additional teacher in the distillation process, alongside the diffusion model. That said, a more recent iteration of consistency models24 does not use EMA.
Another strategy to improve consistency models is to use alternative loss functions for distillation, such as a perceptual loss like LPIPS19, instead of the usual mean squared error (MSE), which we’ve also seen used before with rectified flow17.
Recent work on distilling a Stable Diffusion model into a latent consistency model25 has yielded compelling results, producing high-resolution images in 1 to 4 sampling steps.
Consistency trajectory models26 are a generalisation of both diffusion models and consistency models, enabling prediction of any point along a path from any other point before it, as well as tangent directions. To achieve this, they are conditioned on two time steps, indicating the start and end positions. When both time steps are the same, the model predicts the tangent direction, like a diffusion model would.
BOOT: data-free distillation
Instead of predicting the endpoint of a path at the data side from any point on that path, as consistency models learn to do, we can try to predict any point on the path from its endpoint at the noise side. This is what BOOT27 does, providing yet another way to describe a mapping between noise and data. Comparing this formulation to consistency models, one looks like the “transpose” of the other (see diagram below). For those of you who remember word2vec28, it reminds me lot of the relationship between the skip-gram and continuous bag-of-words (CBoW) methods!
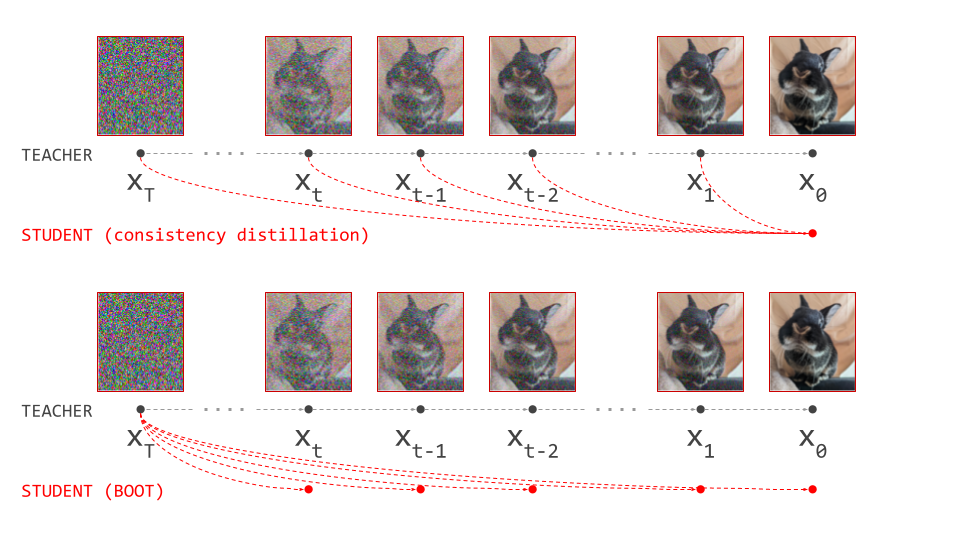
Just like consistency models, this formulation enables a form of bootstrapping to avoid having to run the full sampling procedure using the teacher (hence the name, I presume): predict \(\mathbf{x}_t = f(\varepsilon, t)\) using the student, run a teacher sampling step to obtain \(\mathbf{x}_{t - \Delta t}\), then train the student so that \(f(\varepsilon, t - \Delta t) \equiv \mathbf{x}_{t - \Delta t}\).
Because the student only ever takes the noise \(\varepsilon\) as input, we do not need any training data to perform distillation. This is also the case when we directly distill the diffusion sampling procedure into a single forward pass – though of course in that case, we can’t avoid running the full sampling procedure using the teacher.
There is one big caveat however: it turns out that predicting \(\mathbf{x}_t\) is actually quite hard to learn. But there is a neat workaround for this: instead of predicting \(\mathbf{x}_t\) directly, we first convert it into a different target using the identity \(\mathbf{x}_t = \alpha_t \mathbf{x}_0 + \sigma_t \varepsilon\). Since \(\varepsilon\) is given, we can rewrite this as \(\mathbf{x}_0 = \frac{\mathbf{x}_t - \sigma_t \varepsilon}{\alpha_t}\), which corresponds to an estimate of the clean input. Whereas \(\mathbf{x}_t\) looks like a noisy image, this single-step \(\mathbf{x}_0\) estimate looks like a blurry image instead, lacking high-frequency content. This is a lot easier for a neural network to predict.
If we see \(\mathbf{x}_t\) as a mixture of signal and noise, we are basically extracting the “signal” component and predicting that instead. We can easily convert such a prediction back to a prediction of \(\mathbf{x}_t\) using the same formula. Just like \(\mathbf{x}_t\) traces a path through input space which can be described by an ODE, this time-dependent \(\mathbf{x}_0\)-estimate does as well. The BOOT authors call the ODE describing this path the signal-ODE.
Unlike in the original consistency models formulation (as well as TRACT), no exponential moving average is used for the bootstrapping procedure. To reduce error accumulation, the authors suggest using a higher-order solver to run the teacher sampling step. Another requirement to make this method work well is an auxiliary “boundary loss”, ensuring the distilled model is well-behaved at \(t = T\) (i.e. at the highest noise level).
Sampling with neural operators
Diffusion sampling with neural operators (DSNO; also known as DFNO, the acronym seems to have changed at some point!)29 works by training a model that can predict an entire path from noise to data given a noise sample in a single forward pass. While the inputs (\(\varepsilon\)) and targets (\(\mathbf{x}_t\) at various \(t\)) are the same as for a BOOT-distilled student model, the latter is only able to produce a single point on the path at a time.
This seems ambitious – how can a neural network predict an entire path at once, from noise all the way to data? The so-called Fourier neural operator (FNO)30 is used to achieve this. By imposing certain architectural constraints, adding temporal convolution layers and making use of the Fourier transform to represent functions of time in frequency space, we obtain a model that can produce predictions for any number of time steps at once.
A natural question is then: why would we actually want to predict the entire path? When sampling, we only really care about the final outcome, i.e. the endpoint of the path at the data side (\(t = 0\)). For BOOT, the point of predicting the other points on the path is to enable the bootstrapping mechanism used for training. But DSNO does not involve any bootstrapping, so what is the point of doing this here?
The answer probably lies in the inductive bias of the temporal convolution layers, combined with the relative smoothness of the paths through input space learnt by diffusion models. Thanks to this architectural prior, training on other points on the path also helps to improve the quality of the predictions at the endpoint on the data side, that is, the only point on the path we actually care about when sampling in a single step. I have to admit I am not 100% confident that this is the only reason – if there is another compelling reason why this works, please let me know!
Score distillation sampling
Score distillation sampling (SDS)31 is a bit different from the methods we’ve discussed so far: rather than accelerating sampling by producing a student model that needs fewer steps for high-quality output, this method is aimed at optimisation of parameterised representations of images. This means that it enables diffusion models to operate on other representations of images than pixel grids, even though that is what they were trained on – as long as those representations produce pixel space outputs that are differentiable w.r.t. their parameters32.
As a concrete example of this, SDS was actually introduced to enable text-to-3D. This is achieved through optimisation of Neural Radiance Field (NeRF)33 representations of 3D models, using a pretrained image diffusion model applied to random 2D projections to control the generated 3D models through text prompts (DreamFusion).
Naively, one could think that simply backpropagating the diffusion loss at various time steps through the pixel space output produced by the parameterised representation should do the trick. This yields gradient updates w.r.t. the representation parameters that minimise the diffusion loss, which should make the pixel space output look more like a plausible image. Unfortunately, this method doesn’t work very well, even when applied directly to pixel representations.
It turns out this is primarily caused by a particular factor in the gradient, which corresponds to the Jacobian of the diffusion model itself. This Jacobian is poorly conditioned for low noise levels. Simply omitting this factor altogether (i.e. replacing it with the identity matrix) makes things work much better. As an added bonus, it means we can avoid having to backpropagate through the diffusion model. All we need is forward passes, just like in regular diffusion sampling algorithms!
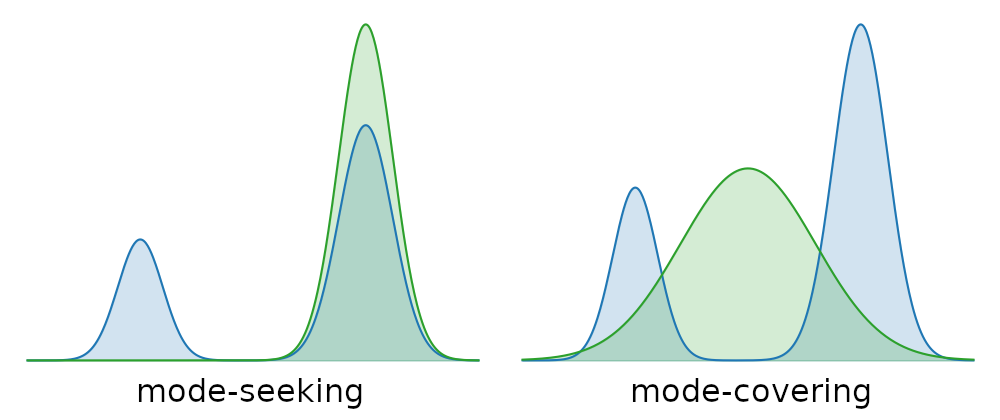
After modifying the gradient in a fairly ad-hoc fashion, it’s worth asking what loss function this modified gradient corresponds to. This is actually the same loss function used in probability density distillation34, which was originally developed to distill autoregressive models for audio waveform generation into feedforward models. I won’t elaborate on this connection here, except to mention that it provides an explanation for the mode-seeking behaviour that SDS seems to exhibit. This behaviour often results in pathologies, which require additional regularisation loss terms to mitigate. It was also found that using a high guidance scale for the teacher (a higher value than one would normally use to sample images) helps to improve results.
Noise-free score distillation (NFSD)35 is a variant that modifies the gradient further to enable the use of lower guidance scales, which results in better sample quality and diversity. Variational score distillation sampling (VSD)36 improves over SDS by optimising a distribution over parameterised representations, rather than a point estimate, which also eliminates the need for high guidance scales.
VSD has in turn been used as a component in more traditional diffusion distillation strategies, aimed at reducing the number of sampling steps. A single-step image generator can easily be reinterpreted as a distribution over parameterised representations, which makes VSD readily applicable to this setting, even if it was originally conceived to improve text-to-3D rather than speed up image generation.
Diff-Instruct37 can be seen as such an application, although it was actually published concurrently with VSD. To distill the knowledge from a diffusion model into a single-step feed-forward generator, they suggest minimising the integral KL divergence (IKL), which is a weighted integral of the KL divergence along the diffusion process (w.r.t. time). Its gradient is estimated by contrasting the predictions of the teacher and those of an auxiliary diffusion model which is concurrently trained on generator outputs. This concurrent training gives it a bit of a GAN38 flavour, but note that the generator and the auxiliary model are not adversaries in this case. As with SDS, the gradient of the IKL with respect to the generator parameters only requires evaluating the diffusion model teacher, but not backpropagating through it – though training the auxiliary diffusion model on generator outputs does of course require backpropagation.
Distribution matching distillation (DMD)39 arrives at a very similar formulation from a different angle. Just like in Diff-Instruct, a concurrently trained diffusion model of the generator outputs is used, and its predictions are contrasted against those of the teacher to obtain gradients for the feed-forward generator. This is combined with a perceptual regression loss (LPIPS19) on paired data from the teacher, which is pre-generated offline. The latter is only applied on a small subset of training examples, making the computational cost of this pre-generation step less prohibitive.
Adversarial distillation
Before diffusion models completely took over in the space of image generation, generative adversarial networks (GANs)38 offered the best visual fidelity, at the cost of mode-dropping: the diversity of model outputs usually does not reflect the diversity of the training data, but at least they look good. In other words, they trade off diversity for quality. On top of that, GANs generate images in a single forward pass, so they are very fast – much faster than diffusion model sampling.
It is therefore unsurprising that some works have sought to combine the benefits of adversarial models and diffusion models. There are many ways to do so: denoising diffusion GANs40 and adversarial score matching41 are just two examples.
A more recent example is UFOGen42, which proposes an adversarial finetuning approach for diffusion models that looks a lot like distillation, but actually isn’t distillation, in the strict sense of the word. UFOGen combines the standard diffusion loss with an adversarial loss. Whereas the standard diffusion loss by itself would result in a model that tries to predict the conditional expectation \(\mathbb{E}\left[\mathbf{x}_0 \mid \mathbf{x}_t \right]\), the additional adversarial loss term allows the model to deviate from this and produce less blurry predictions at high noise levels. The result is a reduction in diversity, but it also enables faster sampling. Both the generator and the discriminator are initialised from the parameters of a pre-trained diffusion model, but this pre-trained model is not evaluated to produce training targets, as would be the case in a distillation approach. Nevertheless, it merits inclusion here, as it is intended to achieve the same goal as most of the distillation approaches that we’ve discussed.
Adversarial diffusion distillation43, on the other hand, is a “true” distillation approach, combining score distillation sampling (SDS) with an adversarial loss. It makes use of a discriminator built on top of features from an image representation learning model, DINO44, which was previously also used for a purely adversarial text-to-image model, StyleGAN-T45. The resulting student model enables single-step sampling, but can also be sampled from with multiple steps to improve the quality of the results. This method was used for SDXL Turbo, a text-to-image system that enables realtime generation – the generated image is updated as you type.
But what about “no free lunch”?

Why is it that we can get these distilled models to produce compelling samples in just a few steps, when diffusion models take tens or hundreds of steps to achieve the same thing? What about “no such thing as a free lunch”?
At first glance, diffusion distillation certainly seems like a counterexample to what is widely considered a universal truth in machine learning, but there is more to it. Up to a point, diffusion model sampling can probably be made more efficient through distillation at no noticeable cost to model quality, but the regime targeted by most distillation methods (i.e. 1-4 sampling steps) goes far beyond that point, and trades off quality for speed. Distillation is almost always “lossy” in practice, and the student cannot be expected to perfectly mimic the teacher’s predictions. This results in errors which can accumulate across sampling steps, or for some methods, across different phases of the distillation process.
What does this trade-off look like? That depends on the distillation method. For most methods, the decrease in model quality directly affects the perceptual quality of the output: samples from distilled models can often look blurry, or the fine-grained details might look sharp but less realistic, which is especially noticeable in images of human faces. The use of adversarial losses based on discriminators, or perceptual loss functions such as LPIPS19, is intended to mitigate some of this degradation, by further focusing model capacity on signal content that is perceptually relevant.
Some methods preserve output quality and fidelity of high-frequency content to a remarkable degree, but this then usually comes at cost to the diversity of the samples instead. The adversarial methods discussed earlier are a great example of this, as well as methods based on score distillation sampling, which implicitly optimise a mode-seeking loss function.
So if distillation implies a loss of model quality, is training a diffusion model and then distilling it even worthwhile? Why not train a different type of model instead, such as a GAN, which produces a single-step generator out of the box, without requiring distillation? The key here is that distillation provides us with some degree of control over this trade-off. We gain flexibility: we get to choose how many steps we can afford, and by choosing the right method, we can decide exactly how we’re going to cut corners. Do we care more about fidelity or diversity? It’s our choice!
Do we really need a teacher?

Once we have established that diffusion distillation gives us the kind of model that we are after, with the right trade-offs in terms of output quality, diversity and sampling speed, it’s worth asking whether we even needed distillation to arrive at this model to begin with. In a sense, once we’ve obtained a particular model through distillation, that’s an existence proof, showing that such a model is feasible in practice – but it does not prove that we arrived at that model in the most efficient way possible. Perhaps there is a shorter route? Could we train such a model from scratch, and skip the training of the teacher model entirely?
The answer depends on the distillation method. For certain types of models that can be obtained through diffusion distillation, there are indeed alternative training recipes that do not require distillation at all. However, these tend not to work quite as well as the distillation route. Perhaps this is not that surprising: it has long been known that when distilling a large neural network into a smaller one, we can often get better results than when we train that smaller network from scratch11. The same phenomenon is at play here, because we are distilling a sampling procedure with many steps into one with considerably fewer steps. If we look at the computational graphs of these sampling procedures, the former is much “deeper” than the latter, so what we’re doing looks very similar to distilling a large model into a smaller one.
One instance where you have the choice of distillation or training from scratch, is consistency models. The paper that introduced them20 describes both consistency distillation and consistency training. The latter requires a few tricks to work well, including schedules for some of the hyperparameters to create a kind of “curriculum”, so it is arguably a bit more involved than diffusion model training.
Charting the maze between data and noise

One interesting perspective on diffusion model training that is particularly relevant to distillation, is that it provides a way to uncover an optimal transport map between distributions46. Through the probability flow ODE formulation2, we can see that diffusion models learn a bijection between noise and data, and it turns out that this mapping is approximately optimal in some sense.
This also explains the observation that different diffusion models trained on similar data tend to learn similar mappings: they are all trying to approximate the same optimum! I tweeted (X’ed?) about this a while back:
With all the recent work on distilling diffusion models into single-pass models, I've been thinking a lot about diffusion model training as solving a kind of optimal transport problem🚐 (1/6)
— Sander Dieleman (@sedielem) December 5, 2023
So far, it seems that diffusion model training is the simplest and most effective (i.e. scalable) way we know of to approximate this optimal mapping, but it is not the only way: consistency training represents a compelling alternative strategy. This makes me wonder what other approaches are yet to be discovered, and whether we might be able to find methods that are even simpler than diffusion model training, or more statistically efficient.
Another interesting link between some of these methods can be found by looking more closely at curvature. The paths connecting samples from the noise and data distributions uncovered by diffusion model training tend to be curved. This is why we need many discrete steps to approximate them accurately when sampling.
We discussed a few approaches to sidestep this issue: consistency models20 21 avoid it by changing the prediction target of the model, from the tangent direction at the current position to the endpoint of the curve at the data side. Rectified flow17 instead replaces the curved paths altogether, with a set of paths that are much straighter. But for perfectly straight paths, the tangent direction will actually point to the endpoint! In other words: in the limiting case of perfectly straight paths, consistency models and diffusion models predict the same thing, and become indistinguishable from each other.
Is that observation practically relevant? Probably not – it’s just a neat connection. But I think it’s worthwhile to cultivate a deeper understanding of deterministic mappings between distributions and how to uncover them at scale, as well as the different ways to parameterise them and represent them. I think this is fertile ground for innovations in diffusion distillation, as well as generative modelling through iterative refinement in a broader sense.
Closing thoughts

As I mentioned at the beginning, this was supposed to be a fairly high-level treatment of diffusion distillation, and why there are so many different ways to do it. I ended up doing a bit of a deep dive, because it’s difficult to talk about the connections between all these methods without also explaining the methods themselves. In reading up on the subject and trying to explain things concisely, I actually learnt a lot. If you want to learn about a particular subject in machine learning research (or really anything else), I can heartily recommend writing a blog post about it.
To wrap things up, I wanted to take a step back and identify a few patterns and trends. Although there is a huge variety of diffusion distillation methods, there are clearly some common tricks and ideas that come back frequently:
- Using deterministic sampling algorithms to obtain targets from the teacher is something that almost all methods rely on. DDIM4 is popular, but more advanced methods (e.g. higher-order methods) are also an option.
- The parameters of the student network are usually initialised from those of the teacher. This doesn’t just accelerate convergence, for some methods this is essential for them to work at all. We can do this because the architectures of the teacher and student are often identical, unlike in distillation of discriminative models.
- Several methods make use of perceptual losses such as LPIPS19 to reduce the negative impact of distillation on low-level perceptual quality.
- Bootstrapping, i.e. having the student learn from itself, is a useful trick to avoid having to run the full sampling algorithm to obtain targets from the teacher. Sometimes using the exponential moving average of the student’s parameters is found to help for this, but this isn’t as clear-cut.
Distillation can interact with other modelling choices. One important example is classifier-free guidance15, which implicitly relies on there being many sampling steps. Guidance operates by modifying the direction in input space predicted by the diffusion model, and the effect of this will inevitably be reduced if only a few sampling steps are taken. For some methods, applying guidance after distillation doesn’t actually make sense anymore, because the student no longer predicts a direction in input space. Luckily guidance distillation16 can be used to mitigate the impact of this.
Another instance of this is latent diffusion47: when applying distillation to a diffusion model trained in latent space, one important question to address is whether the loss should be applied to the latent representation or to pixels. As an example, the adversarial diffusion distillation (ADD) paper43 explicitly suggests calculating the distillation loss in pixel space for improved stability.
The procedure of first solving a problem as well as possible, and then looking for shortcuts that yield acceptable trade-offs, is very effective in machine learning in general. Diffusion distillation is a quintessential example of this. There is still no such thing as a free lunch, but diffusion distillation enables us to cut corners with intention, and that’s worth a lot!
If you would like to cite this post in an academic context, you can use this BibTeX snippet:
@misc{dieleman2024distillation,
author = {Dieleman, Sander},
title = {The paradox of diffusion distillation},
url = {https://sander.ai/2024/02/28/paradox.html},
year = {2024}
}
Acknowledgements
Thanks once again to Bundle the bunny for modelling, and to kipply for permission to use this photograph. Thanks to Emiel Hoogeboom, Valentin De Bortoli, Pierre Richemond, Andriy Mnih and all my colleagues at Google DeepMind for various discussions, which continue to shape my thoughts on diffusion models and beyond!
References
-
Ho, Jain, Abbeel, “Denoising Diffusion Probabilistic Models”, 2020. ↩ ↩2
-
Song, Sohl-Dickstein, Kingma, Kumar, Ermon and Poole, “Score-Based Generative Modeling through Stochastic Differential Equations”, International Conference on Learning Representations, 2021. ↩ ↩2 ↩3
-
Karras, Aittala, Aila, Laine, “Elucidating the Design Space of Diffusion-Based Generative Models”, Neural Information Processing Systems, 2022. ↩ ↩2 ↩3
-
Song, Meng, Ermon, “Denoising Diffusion Implicit Models”, International Conference on Learning Representations, 2021. ↩ ↩2 ↩3
-
Jolicoeur-Martineau, Li, Piché-Taillefer, Kachman, Mitliagkas, “Gotta Go Fast When Generating Data with Score-Based Models”, arXiv, 2021. ↩
-
Dockhorn, Vahdat, Kreis, “GENIE: Higher-Order Denoising Diffusion Solvers”, Neural Information Processing Systems, 2022. ↩
-
Liu, Ren, Lin, Zhao, “Pseudo Numerical Methods for Diffusion Models on Manifolds”, International Conference on Learning Representations, 2022. ↩
-
Zhang, Chen, “Fast Sampling of Diffusion Models with Exponential Integrator”, International Conference on Learning Representations, 2023. ↩
-
Lu, Zhou, Bao, Chen, Li, Zhu, “DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps”, Neural Information Processing Systems, 2022. ↩
-
Lu, Zhou, Bao, Chen, Li, Zhu, “DPM-Solver++: Fast Solver for Guided Sampling of Diffusion Probabilistic Models”, arXiv, 2022. ↩
-
Hinton, Vinyals, Dean, “Distilling the Knowledge in a Neural Network”, NeurIPS Deep Learning Workshop, 2014. ↩ ↩2
-
Luo, “A Comprehensive Survey on Knowledge Distillation of Diffusion Models”, arXiv, 2023. ↩
-
Luhman, Luhman, “Knowledge Distillation in Iterative Generative Models for Improved Sampling Speed”, arXiv, 2021. ↩
-
Salimans, Ho, “Progressive Distillation for Fast Sampling of Diffusion Models”, International Conference on Learning Representations, 2022. ↩
-
Ho, Salimans, “Classifier-Free Diffusion Guidance”, Neural Information Processing Systems, 2021. ↩ ↩2
-
Meng, Rombach, Gao, Kingma, Ermon, Ho, Salimans, “On Distillation of Guided Diffusion Models”, Computer Vision and Pattern Recognition, 2023. ↩ ↩2
-
Liu, Gong, Liu, “Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow”, International Conference on Learning Representations, 2023. ↩ ↩2 ↩3
-
Liu, Zhang, Ma, Peng, Liu, “InstaFlow: One Step is Enough for High-Quality Diffusion-Based Text-to-Image Generation”, arXiv, 2023. ↩
-
Zhang, Isola, Efros, Shechtman, Wang, “The Unreasonable Effectiveness of Deep Features as a Perceptual Metric”, Computer Vision and Pattern Recognition, 2018. ↩ ↩2 ↩3 ↩4 ↩5
-
Song, Dhariwal, Chen, Sutskever, “Consistency Models”, International Conference on Machine Learning, 2023. ↩ ↩2 ↩3
-
Berthelot, Autef, Lin, Yap, Zhai, Hu, Zheng, Talbott, Gu, “TRACT: Denoising Diffusion Models with Transitive Closure Time-Distillation”, arXiv, 2023. ↩ ↩2
-
Song, Ermon, “Improved Techniques for Training Score-Based Generative Models”, Neural Information Processing Systems, 2020. ↩
-
Karras, Aittala, Lehtinen, Hellsten, Aila, Laine, “Analyzing and Improving the Training Dynamics of Diffusion Models”, arXiv, 2023. ↩
-
Song, Dhariwal, “Improved Techniques for Training Consistency Models”, International Conference on Learnign Representations, 2024. ↩
-
Luo,Tan, Huang, Li, Zhao, “Latent Consistency Models: Synthesizing High-Resolution Images with Few-Step Inference”, arXiv, 2023. ↩
-
Kim, Lai, Liao, Murata, Takida, Uesaka, He, Mitsufuji, Ermon, “Consistency Trajectory Models: Learning Probability Flow ODE Trajectory of Diffusion”, International Conference on Learning Representations, 2024. ↩
-
Gu, Zhai, Zhang, Liu, Susskind, “BOOT: Data-free Distillation of Denoising Diffusion Models with Bootstrapping”, arXiv, 2023. ↩
-
Mikolov, Chen, Corrado, Dean, “Efficient Estimation of Word Representations in Vector Space”, International Conference on Learning Representation, 2013. ↩
-
Zheng, Nie, Vahdat, Azizzadenesheli, Anandkumar, “Fast Sampling of Diffusion Models via Operator Learning”, International Conference on Machine Learning, 2023. ↩
-
Li, Kovachki, Azizzadenesheli, Liu, Bhattacharya, Stuart, Anandkumar, “Fourier neural operator for parametric partial differential equations”, International Conference on Learning Representations, 2021. ↩
-
Poole, Jain, Barron, Mildenhall, “DreamFusion: Text-to-3D using 2D Diffusion”, arXiv, 2022. ↩
-
Mordvintsev, Pezzotti, Schubert, Olah, “Differentiable Image Parameterizations”, Distill, 2018. ↩
-
Mildenhall, Srinivasan, Tancik, Barron, Ramamoorthi, Ng, “NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis”, European Conference on Computer Vision, 2020. ↩
-
Van den Oord, Li, Babuschkin, Simonyan, Vinyals, Kavukcuoglu, van den Driessche, Lockhart, Cobo, Stimberg, Casagrande, Grewe, Noury, Dieleman, Elsen, Kalchbrenner, Zen, Graves, King, Walters, Belov and Hassabis, “Parallel WaveNet: Fast High-Fidelity Speech Synthesis”, International Conference on Machine Learning, 2018. ↩
-
Katzir, Patashnik, Cohen-Or, Lischinski, “Noise-free Score Distillation”, International Conference on Learning Representations, 2024. ↩
-
Wang, Lu, Wang, Bao, Li, Su, Zhu, “ProlificDreamer: High-Fidelity and Diverse Text-to-3D Generation with Variational Score Distillation”, Neural Information Processing Systems, 2023. ↩
-
Luo, Hu, Zhang, Sun, Li, Zhang, “Diff-Instruct: A Universal Approach for Transferring Knowledge From Pre-trained Diffusion Models”, Neural Information Processing Systems, 2023. ↩
-
Goodfellow, Pouget-Abadie, Mirza, Xu, Warde-Farley, Ozair, Courville and Bengio, “Generative Adversarial Nets”, Neural Information Processing Systems, 2014. ↩ ↩2
-
Yin, Gharbi, Zhang, Shechtman, Durand, Freeman, Park, “One-step Diffusion with Distribution Matching Distillation”, arXiv, 2023. ↩
-
Xiao, Kreis, Vahdat, “Tackling the Generative Learning Trilemma with Denoising Diffusion GANs”, International Conference on Learning Representations, 2022. ↩
-
Jolicoeur-Martineau, Piché-Taillefer, Tachet des Combes, Mitliagkas, “Adversarial score matching and improved sampling for image generation”, International Conference on Learning Representations, 2021. ↩
-
Xu, Zhao, Xiao, Hou, “UFOGen: You Forward Once Large Scale Text-to-Image Generation via Diffusion GANs”, arXiv, 2023. ↩
-
Sauer, Lorenz, Blattmann, Rombach, “Adversarial Diffusion Distillation”, arXiv, 2023. ↩ ↩2
-
Caron, Touvron, Misra, Jégou, Mairal, Bojanowski, Joulin, “Emerging Properties in Self-Supervised Vision Transformers”, International Conference on Computer Vision, 2021. ↩
-
Sauer, Karras, Laine, Geiger, Aila, “StyleGAN-T: Unlocking the Power of GANs for Fast Large-Scale Text-to-Image Synthesis”, International Conference on Machine Learning, 2023. ↩
-
Khrulkov, Ryzhakov, Chertkov, Oseledets, “Understanding DDPM Latent Codes Through Optimal Transport”, International Conference on Learning Representations, 2023. ↩
-
Rombach, Blattmann, Lorenz, Esser, Ommer, “High-Resolution Image Synthesis with Latent Diffusion Models”, Computer Vision and Pattern Recognition, 2022. ↩